Is 0 Even - Clearing Up The Number Mystery

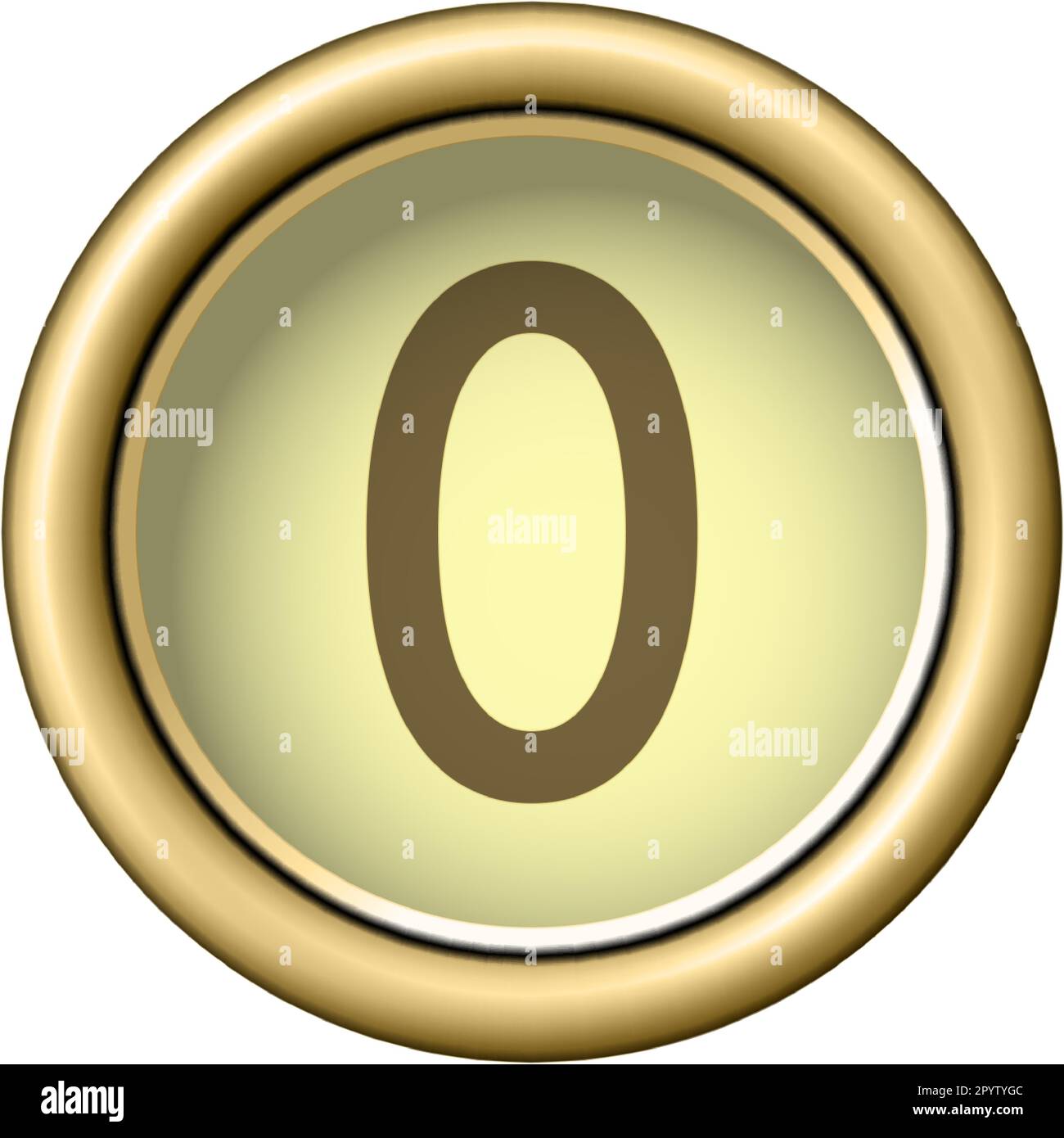
Have you ever stopped to think about the number zero? It’s kind of a big deal, isn't it? For many of us, it feels like a starting point, a placeholder, or maybe just nothing at all. But when someone asks, "is 0 even?" a lot of people might pause, scratch their heads, or even give a quick "no." It’s a question that, in a way, seems to trip people up, and that’s perfectly understandable. This little number, zero, holds a special spot in our counting system, yet its very nature can feel a bit puzzling, especially when we try to sort it into neat groups like 'even' or 'odd.'

It turns out that figuring out whether zero fits into the "even" category is not just a random math question; it helps us get a firmer grasp on how numbers work. There are some straightforward ways to think about this, and, you know, once you see the patterns, it becomes quite clear. We often learn about even numbers as those that pair up nicely, or numbers you can split right down the middle without anything left over. But how does that idea apply to zero, a number that, in some respects, represents the absence of quantity?

So, let's just take a moment to look at this more closely. We'll explore the common ways we define even numbers and see how zero stacks up against those definitions. By the end of this, you might find that your view on this humble number changes a little, and you'll have some good ways to explain why zero truly belongs in the "even" group, clearing up any confusion about "is 0 even."

• Monopoly Go Dice
• Chicken Ranch Nevada
• Princess Emily Age
• Hyatt Cambridge Md
• Sex Memes

Table of Contents

• The Big Question - Is 0 Even?
• How Do We Define Even Numbers? To Understand Is 0 Even
• What Happens When You Divide 0 by 2? To Understand Is 0 Even
• Does 0 Fit the Pattern of Even Numbers? To Understand Is 0 Even
• Is 0 Even a Number at All?
• Practical Applications of 0 Being Even
• Some Common Questions About Is 0 Even
• Clearing Up the Confusion About Is 0 Even

The Big Question - Is 0 Even?

The question of whether zero is an even number comes up quite a bit. It's a topic that, you know, can spark a little debate, even among people who are pretty good with numbers. Some folks might instantly say "yes," while others might hesitate, thinking it's neither one nor the other. But when we look at the standard ways we talk about numbers, especially in mathematics, zero really does fit the description of an even number. It's not just a matter of convention, either; there are very good reasons for this classification. So, when someone asks, "is 0 even?", the straightforward answer, based on how numbers work, is "yes."

To grasp why zero is considered an even number, we need to think about what makes any number even. It's a bit like sorting items into different baskets. We have rules for what goes into the "even" basket and what goes into the "odd" basket. Zero, in fact, meets all the requirements for the "even" basket, which is pretty neat. It’s not some kind of exception or a special case that we just decide to put there; it genuinely behaves like all the other even numbers we know.

This might seem a little surprising to some, especially if they've always thought of even numbers as positive numbers like 2, 4, or 6. But numbers can be negative too, and zero sits right there in the middle, connecting the positive and negative sides of the number line. Understanding its place as an even number helps us build a more complete picture of how our number system works, and that's, you know, pretty useful.

• Usc Mind Challenge
• Steffy Moreno Videos
• Lily Starfire
• Joe Penny
• Chris Brown Net Worth

How Do We Define Even Numbers? To Understand Is 0 Even

Before we can truly answer "is 0 even?", we need to get clear on what an even number actually is. There are a few main ways we talk about even numbers, and all of them point to zero being even. One common way to think about it is that an even number is any whole number that you can divide by two, and the answer you get is also a whole number, with no bits left over. So, for example, if you take 6 and divide it by 2, you get 3, which is a whole number. This makes 6 an even number.

Another way people define an even number is that it is a multiple of two. This means you can get to that number by multiplying two by some other whole number. So, for instance, 8 is a multiple of two because 2 times 4 gives you 8. This definition, too, is very helpful for figuring out "is 0 even?". If a number has two as a factor, meaning it can be made by multiplying two by something, then it's even.

A third way to spot an even number, especially when you're looking at bigger numbers, is to check its very last digit. If the last digit of a number is 0, 2, 4, 6, or 8, then that number is an even number. For example, 124 ends in a 4, so it's even. The number 350 ends in a 0, so it's even. This is a quick trick, and it also gives us a pretty strong hint about "is 0 even."

All these definitions, whether you're thinking about dividing, multiplying, or just looking at the last digit, are consistent. They all lead to the same conclusion about zero. It's not like one definition says zero is even and another says it's odd; they all agree, which is, you know, quite reassuring when you're trying to figure something out in math.

What Happens When You Divide 0 by 2? To Understand Is 0 Even

One of the most straightforward ways to figure out "is 0 even?" is to use that first definition we talked about: can you divide it by two without any remainder? So, let's try it with zero. If you have zero items and you want to share them equally between two people, how many items does each person get? Well, each person gets zero items. When you divide 0 by 2, the answer you get is 0.

And here's the key part: 0 is a whole number. It's an integer, just like 1, 2, 3, or -1, -2, -3. Since the result of dividing 0 by 2 is a whole number (0 itself), this completely fits the definition of an even number. There's nothing left over, no fraction, no decimal part. It divides perfectly, which is what we look for when we're trying to see if a number is even. This makes the case for "is 0 even" pretty strong, don't you think?

Think about it this way: if you have 4 cookies and divide them by 2, you get 2 cookies for each person. If you have 2 cookies and divide them by 2, you get 1 cookie for each person. If you have 0 cookies and divide them by 2, you get 0 cookies for each person. The pattern holds up beautifully. This simple arithmetic, in a way, really helps clear up any confusion about "is 0 even." It shows that zero behaves just like other even numbers when it comes to division.

Does 0 Fit the Pattern of Even Numbers? To Understand Is 0 Even

Numbers on the number line have a very clear pattern when it comes to being even or odd. They alternate, one after the other. You have an odd number, then an even number, then an odd number, then an even number, and so on. For example, if you start at 1 (odd), then 2 (even), then 3 (odd), then 4 (even). This pattern goes both ways, meaning it works for numbers getting smaller too.

So, if we look at the numbers around zero, what do we see? On one side, you have -1, and on the other side, you have 1. Both -1 and 1 are odd numbers. Since the numbers on either side of zero are odd, then zero itself must be an even number to keep that alternating pattern going. It's a pretty neat way to confirm "is 0 even" without even doing any division. This pattern is very consistent across all integers.

This alternating pattern is a very important property of how even and odd numbers work together. It's not just a coincidence; it's how the number line is structured. Zero fits right into that structure, keeping the sequence smooth and predictable. If zero were odd, or neither, the whole pattern would, you know, fall apart right there in the middle, which would make things much less orderly. So, the number line itself provides pretty good evidence for "is 0 even."

Another way to think about patterns is how we often define numbers recursively, meaning we define them based on numbers that come before them. Natural even numbers are often defined starting from zero and then adding two repeatedly. Zero is the starting point for this definition, which further supports its classification as an even number. This is, you know, quite a foundational idea in mathematics.

Is 0 Even a Number at All?

Sometimes, people might wonder, "is 0 even a number?" This is a very old question, actually. For a long time, early humans found it hard to think about "nothing" as a quantity you could count. You can count dogs, you know, but how do you count an empty space? The idea of zero, as a number representing no amount or objects, was not always as natural to people as it is to us now. It took a long time for the concept of zero to be fully accepted and used in mathematics around the world.

But in modern mathematics, zero is absolutely considered a number. It's a very important number, actually. It acts as the additive identity, meaning if you add zero to any number, that number stays the same. It's also the point where positive and negative numbers meet on the number line. Zero is neither positive nor negative, but it is a real number, and it is an integer. So, yes, it is definitely a number, and a very useful one at that.

Once we accept that zero is indeed a number, then the question of "is 0 even?" becomes a lot simpler to answer using the definitions and patterns we've already discussed. Any confusion about whether zero is even often stems from this deeper, older question about whether zero counts as a number in the first place. But for all practical purposes in math today, zero is a full-fledged member of the number family.

Practical Applications of 0 Being Even

Knowing that zero is an even number isn't just a fun math fact; it has real-world implications and is important in various fields, like computer science and even in everyday rules. For example, you know, after Superstorm Sandy, the mayor of New York City, Michael Bloomberg, made a rule about filling up cars with gasoline. He said that cars with even-numbered license plates could only get gas on even dates. And, very importantly, he specified that zero was to count as an even number for this rule. This shows how this mathematical definition plays a role in practical, real-life situations.

In computer science, too, understanding the parity of zero is pretty fundamental. When programmers work with numbers, especially in things like indexing arrays (lists of items), they often start counting from zero. Knowing whether zero is even or odd can affect how certain algorithms work or how data is processed. So, it's not just an abstract concept; it has actual, you know, functional importance in how technology operates.

The definition of evenness is consistent across different areas of mathematics and computer science because it creates a system that works without contradictions. If zero were considered odd, or neither, it would cause problems in these systems, leading to logical inconsistencies. For instance, if you're checking a number's parity by its last digit, zero clearly ends in a 0, which is one of the digits for even numbers. This consistency is, you know, quite valuable.

Some Common Questions About Is 0 Even

People often ask similar questions when they're trying to figure out "is 0 even?" One common thought is, "What evidence could even suggest it's an odd number?" And the truth is, there isn't really any strong mathematical evidence to suggest zero is odd. Odd numbers, by definition, have a remainder of 1 when divided by 2. Zero, as we've seen, has a remainder of 0. So, it just doesn't fit the description of an odd number at all.

Another question that sometimes comes up relates to division by zero. Some might think, "If 0 is even, and it's the smallest even absolute value number, do we divide by 0 instead of 2 to check its parity?" This is a misunderstanding. The rule for checking evenness is always about divisibility by 2, not by the number itself. Division by zero is a completely different concept in mathematics, which is undefined, and it doesn't apply to checking a number's parity. So, that's, you know, a different mathematical idea altogether.

People might also ask, "Is 0 odd or even or nothing?" As we've discussed, zero is definitely a number, and it fits all the criteria to be an even number. It's not "nothing" in the sense of not being a number, nor is it "nothing" in the sense of having no parity. It has a very specific parity, and that parity is even. This helps us, you know, put it clearly in its place within our number system.

The idea that zero is "by convention" even sometimes comes up too, as if it's just a rule we decided to make up. While conventions are part of math, this particular classification is not arbitrary. It's based on how zero behaves with respect to the definitions of even and odd numbers, and how it fits into the broader structure of our number system. It's a logical conclusion, not just a convenient agreement.

Clearing Up the Confusion About Is 0 Even

So, let's just put it plainly: zero is an even number. This isn't a tricky question, and it's not a matter of opinion. The definitions of even and odd numbers are quite clear, and zero fits squarely into the "even" category. Whether you think about dividing by 2, looking at its place on the number line, or seeing it as a multiple of 2, all the evidence points to the same conclusion. It's, you know, pretty consistent across the board.

When zero is divided by 2, the result is 0, which is an integer. This is the core reason. Also, zero's position between two odd numbers (-1 and 1) on the number line means it must be even to maintain the alternating pattern of odd and even numbers. This pattern is very fundamental to how we understand numbers.

Understanding why zero is even helps to solidify our basic number sense. It shows that mathematical definitions are consistent and logical, even for a number that sometimes feels a little different from the others. So, the next time someone asks, "is 0 even?", you can confidently say "yes," and, you know, perhaps even explain why.

Here's a quick recap of why zero is considered an even number:

• Zero can be divided by 2, and the answer (0) is a whole number.
• Zero is a multiple of 2 (2 multiplied by 0 gives 0).
• The last digit of zero is 0, which is a characteristic of even numbers.
• On the number line, zero sits between two odd numbers (-1 and 1), keeping the even-odd pattern.
• Zero is the starting point for defining even numbers recursively (0, 2, 4, 6...).